Make a transformer model by hand

Author: suqi

Reference: I made a transformer by hand (no training!) (vgel.me)

Abstract

本文介绍了如何制作一个Transformer 模型，无需训练，无需显卡

Model Overview

Picking a task

因为我们计划通过手动设计权重来完成我们的模型，所以我们选择一个较为简单的模型任务，但也不能过于简单，如预测“abababab”序列的下一个字符。综合考虑，我们选定的模型任务为：

• 对于输入序列“aabaabaab”，预测下一个字符是 “a” or “b”。

Tokenization scheme

因为我们的模型使用了“a”和“b”两个字符，所以我们只需要设计一个简单的分词器即可：

CHARS = ["a", "b"]
def tokenize(s): return [CHARS.index(c) for c in s]
def untok(tok): return CHARS[tok]

# examples:
tokenize("aabaa") # => [0, 0, 1, 0, 0]
untok(0) # => "a"
untok(1) # => "b"

Model Architecture

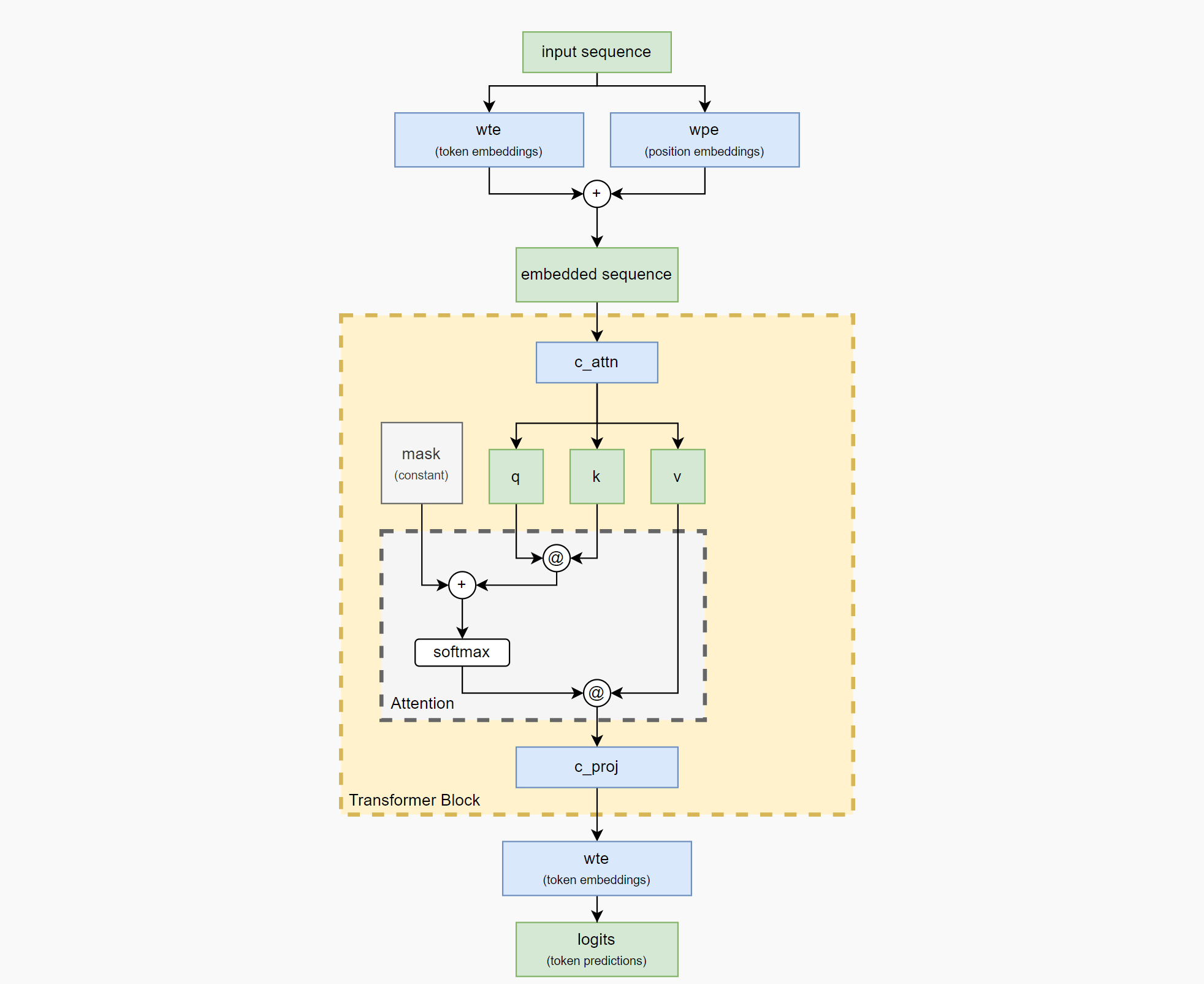
我们选择了类GPT-2的模型架构，具体而言，如下图所示，接下来我将逐一实现这个模型中的每一部分。

Model Parameter

我们需要确定三个模型参数：

• Context length
• Vocabulary size
• Embedding size

Context length是模型一次看到的最大Token数量。理论上，这个任务只需要前面的 2 个Token，但我们使用 5 个Token来让它变得更困难一些，因此我们还需要忽略不相关的Token。

Vocabulary size是模型将看到的不同标记的数量。在真实模型中，我们需要在泛化能力（generalization）、要学习的不同token的数量（number of distinct tokens to learn）、上下文长度（context length usage）之间权衡。但是，我们的任务要简单得多，因此在我们的模型中，我们只需要两个标记：( a)0和b( 1) 。

Embedding size是模型将为每个token/position学习的向量的大小，并且也将在内部使用。我相当随意地选择了 8 个，最终正好符合所需的大小。

N_CTX = 5
N_VOCAB = 2
N_EMBED = 8

Embedding block

分词器tokenizer将输入序列aabaabaab转化为Token001001001作为模型输入，我们需要对其进行编码（embedding），也就是说，我们需要将输入为seq_len 的一维矩阵转换为seq_len x embedding_size的二维矩阵.

def gpt(inputs, wte, wpe, blocks):  # [n_seq] -> [n_seq, n_vocab]
  # token + positional embeddings
  x = wte[inputs] + wpe[range(len(inputs))]  # [n_seq] -> [n_seq, n_embd]
  ...

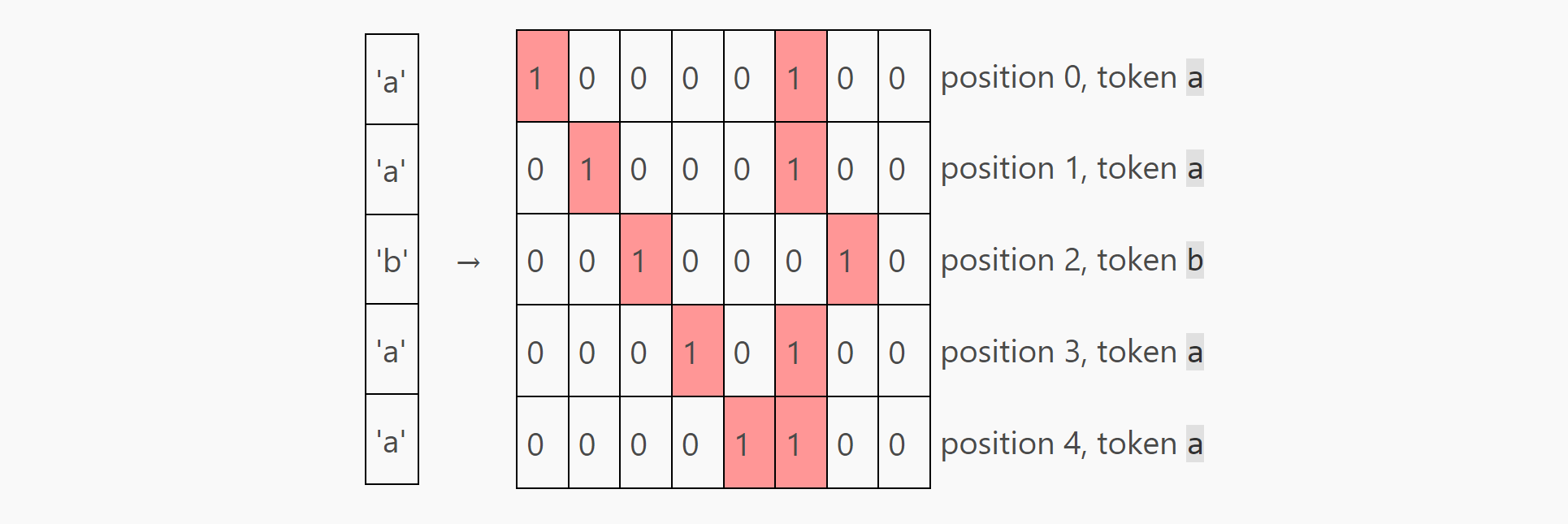
我们要做的第一件事是设计wte（weights for token embeddings）和wpe (weights for position embeddings)。此处我们使用1-hot策略，即对于每个不同的位置使用独立的编码1。在本文中, 我们指定相关编码策略为:

• 使用前五个embedding 元素来表示 position embedding。位置0表示为：[1, 0, 0, 0, 0]，位置1表示为：[0, 1, 0, 0, 0]，直到位置4表示为：[0, 0, 0, 0, 1]。
• 使用接下来两个embedding 元素表示token embedding，token a 表示为 [1, 0], token b 表示为[0, 1]。
• 最后一个位置先暂时忽略, 默认其为0.

也就是说, 如果第3个位置上出现字符”a”, 相关编码为: 00100100 其中00100为position embedding, 后面的10为token embedding.

基于此策略,相关模型权重定义如下:

MODEL = {
  "wte": np.array(
    # one-hot token embeddings
    [
      [0, 0, 0, 0, 0, 1, 0, 0],  # token `a` (id 0)
      [0, 0, 0, 0, 0, 0, 1, 0],  # token `b` (id 1)
    ]
  ),
  "wpe": np.array(
    # one-hot position embeddings
    [
      [1, 0, 0, 0, 0, 0, 0, 0],  # position 0
      [0, 1, 0, 0, 0, 0, 0, 0],  # position 1
      [0, 0, 1, 0, 0, 0, 0, 0],  # position 2
      [0, 0, 0, 1, 0, 0, 0, 0],  # position 3
      [0, 0, 0, 0, 1, 0, 0, 0],  # position 4
    ]
  ),
  ...: ...,
}

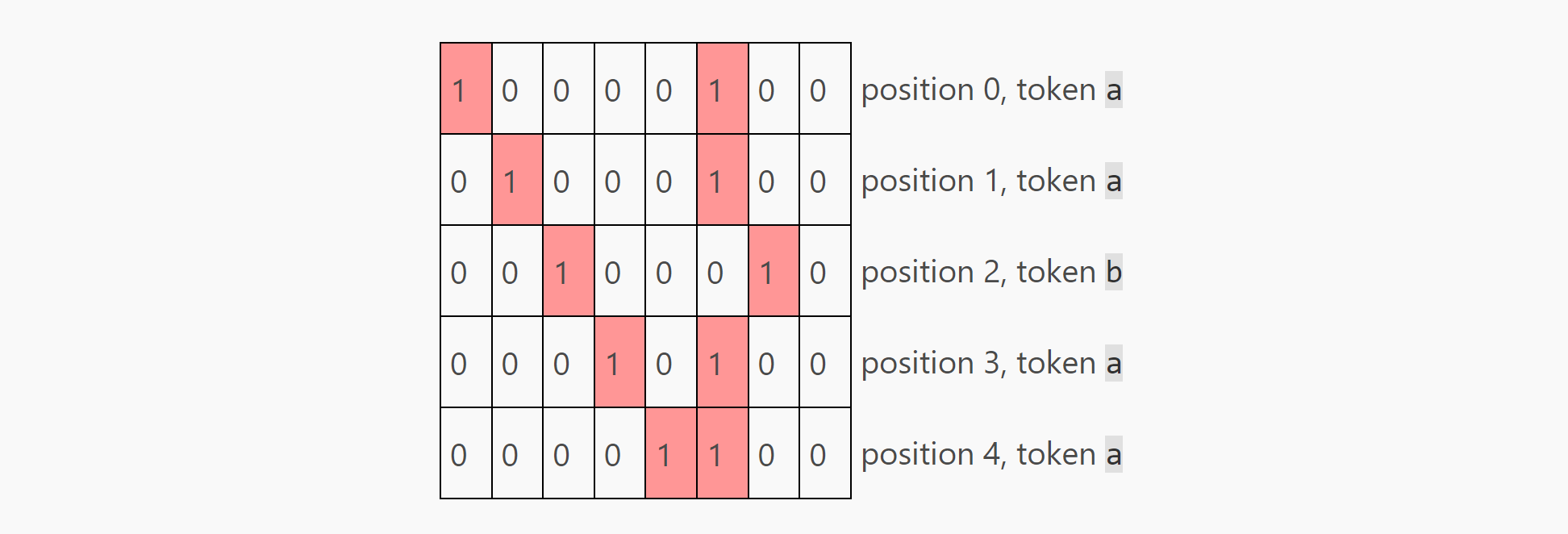
如果我们使用这个策略编码这个序列"aabaa"，我们可以得到下面这个embedding 矩阵，矩阵的大小为 5 x 8 (seq_len x embedding_size)。

接下来我们的模型都基于这个embedding 工作，直到最后投射回vocabulary-space。

注意，第七个embedding的第七个元素并没有使用，这将作为transformer模型中的暂存空间。

Transformer block

目前主流模型都具有多个transformer块, 我们的任务比较简单, 所以我们只使用一个。我们的模型包含两部分：

• 一个注意力头（attention head）.
• 一个线性层（将注意力结果矩阵处理为网络常用的 seq_len x embedding_size大小）。

Attention Layer

在上一节中， 我们得到了embedding 矩阵，embedding 矩阵将作为Attention Layer的输入，Attention Layer完成的工作为：

$$output = softmax(\frac{ Q @ K^T}{np.sqrt(Q.shape[-1])} + MASK) @ V$$​

在我们的代码中定义如下：

# [n_q, d_k], [n_k, d_k], [n_k, d_v], [n_q, n_k] -> [n_q, d_v]
def attention(q, k, v, mask):
  return softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) @ v

其中@表示矩阵乘积操作, 这个公式你暂时无需看懂， 接下来我将逐一介绍其各参数含义.

另外, 在实际训练中，通过 np.sqrt(q.shape[-1]) 进行缩放可以产生更好的梯度，但这对我们的手工制作的 Transformer 没有影响, 所以此处我们不做过多讨论

q/k/v matrix

前文中，我们得到的Embdding matrix为：

我们通过定义一个全连接层c_attn将qkv矩阵分割得到三个大小为seq_len x (embed_size * 3)的矩阵，即q, k, v 三个矩阵, 在我们的模型中，attention的权重在 c_attn中定义：

Lg = 1024 # Large

MODEL = {
  ...: ...,
  "blocks": [
    {
      "attn": {
        "c_attn": {  # generates qkv matrix
          "b": np.zeros(N_EMBED * 3),
          "w": np.array(
            # this is where the magic happens
            # fmt: off
            [
              [Lg, 0., 0., 0., 0., 0., 0., 0.,  # q
                1., 0., 0., 0., 0., 0., 0., 0.,  # k
                  0., 0., 0., 0., 0., 0., 0., 0.], # v
              [Lg, Lg, 0., 0., 0., 0., 0., 0.,  # q
                0., 1., 0., 0., 0., 0., 0., 0.,  # k
                  0., 0., 0., 0., 0., 0., 0., 0.], # v
              [0., Lg, Lg, 0., 0., 0., 0., 0.,  # q
                0., 0., 1., 0., 0., 0., 0., 0.,  # k
                  0., 0., 0., 0., 0., 0., 0., 0.], # v
              [0., 0., Lg, Lg, 0., 0., 0., 0.,  # q
                0., 0., 0., 1., 0., 0., 0., 0.,  # k
                  0., 0., 0., 0., 0., 0., 0., 0.], # v
              [0., 0., 0., Lg, Lg, 0., 0., 0.,  # q
                0., 0., 0., 0., 1., 0., 0., 0.,  # k
                  0., 0., 0., 0., 0., 0., 0., 0.], # v
              [0., 0., 0., 0., 0., 0., 0., 0.,  # q
                0., 0., 0., 0., 0., 0., 0., 0.,  # k
                  0., 0., 0., 0., 0., 0., 0., 1.], # v
              [0., 0., 0., 0., 0., 0., 0., 0.,  # q
                0., 0., 0., 0., 0., 0., 0., 0.,  # k
                  0., 0., 0., 0., 0., 0., 0., -1], # v
              [0., 0., 0., 0., 0., 0., 0., 0.,  # q
                0., 0., 0., 0., 0., 0., 0., 0.,  # k
                  0., 0., 0., 0., 0., 0., 0., 0.], # v
            ]
            # fmt: on
          ),
        },
        ...: ...,
      }
    }
  ]
}

在上面的权重中，我对c_attn不同行上的权重进行了格式化，以显示矩阵的q、k和v是来自于qkv矩阵的哪部分，这看起来似乎很吓人，但是c_attn只是一个常规的全连接层，这个全连接层的维度为： embed_size x (embed_size * 3)。

经过计算 embedding @ c_attn["w"] + c_attn["b"]后，可以得到这个5 x 24 ( seq_len x (embed_size * 3) )的矩阵qkv。（粗线表示我们之后要对矩阵进行的分割操作）

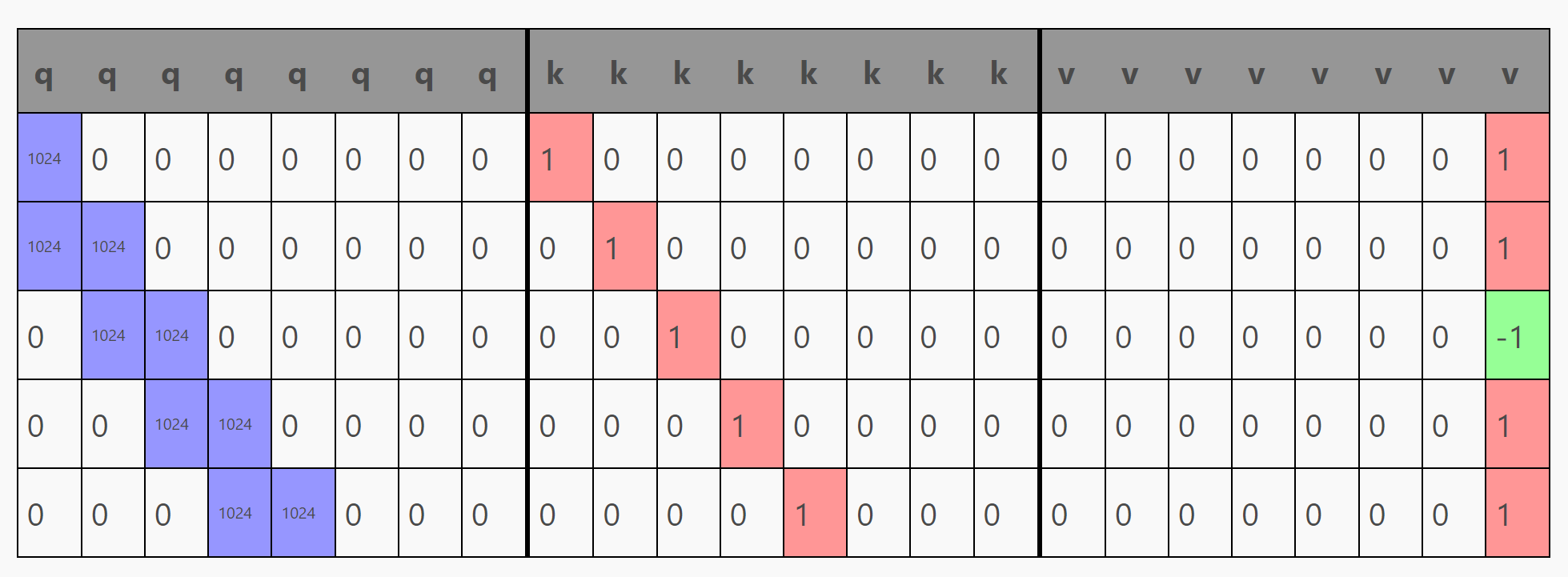
将qkv矩阵分割得到三个大小为seq_len x (embed_size * 3)的矩阵，即q, k, v 三个矩阵.

使用python实现上述内容:

def causal_self_attention(x, c_attn, c_proj):
  # qkv projections
  x = linear(x, **c_attn) # [n_seq, n_embd] -> [n_seq, 3*n_embd]
  # split into qkv
  q, k, v = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> 3 of [n_seq, n_embd]
  ...	

q @ k.T

k的意思应该很明确，是我们之前位置编码的结果，可以认为这是每个token提供的他的位置参数。

但是q是什么？如果说k是每个token提供的，那么q就表示每个token所寻找的。但这在实际中意味着什么？

在attention中，k矩阵会被转置并与被q相乘（ q @ k.T），产生一个 seq_len x seq_len 大小的矩阵，如下图所示：

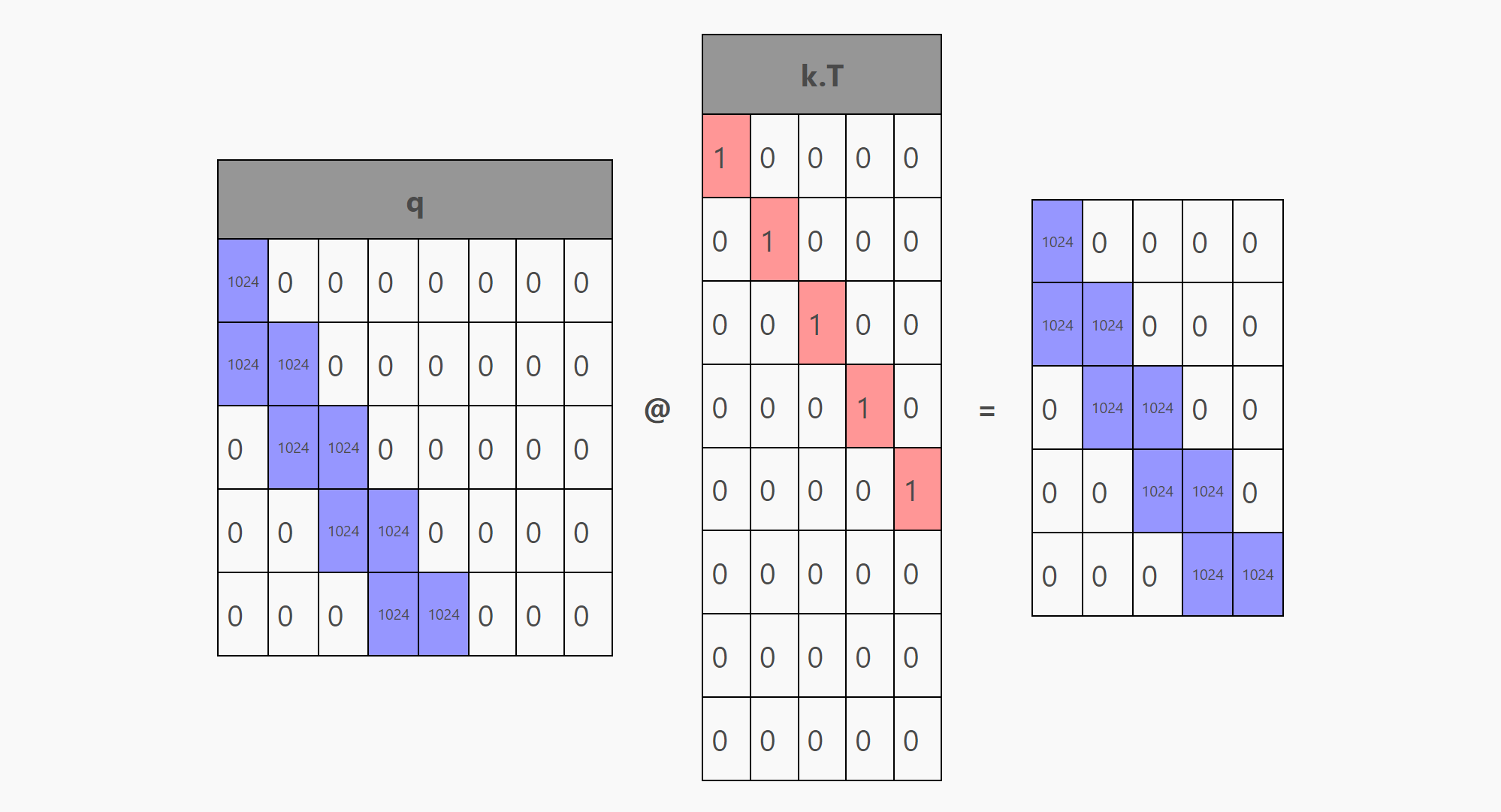
q @ k.T + mask

接下来我们需要添加掩码（mask）,掩码的作用是什么?

mask是为了防止模型看到未来的信息。对于q@k.T, 可以将每一行理解为该行信息需要预测生成的内容（例如：第一行表示模型看到token-0后需要生成的内容），token需要attention每一行的信息。这意味着，第一个预测（第0行）不能关注（attention）除了第0行以外的任意一行，因为第0行只有一个1，其他都是0。

但是对于其他的预测，模型拥有至少两个token去attention，对于aabaabaab任务，只需要两个token即可。所以这个模型将其注意力分割至两个最近的可访问tokens中（没有被masked的token）。这意味着预测第二个token（第1行）需要付出相同的attention道token 0 和token1，以此类推，所以我们可以看到接下来每一行都有两个非0元素（0.5）。

所以，在 q @ k.T + mask中添加的mask就是下面这个矩阵：

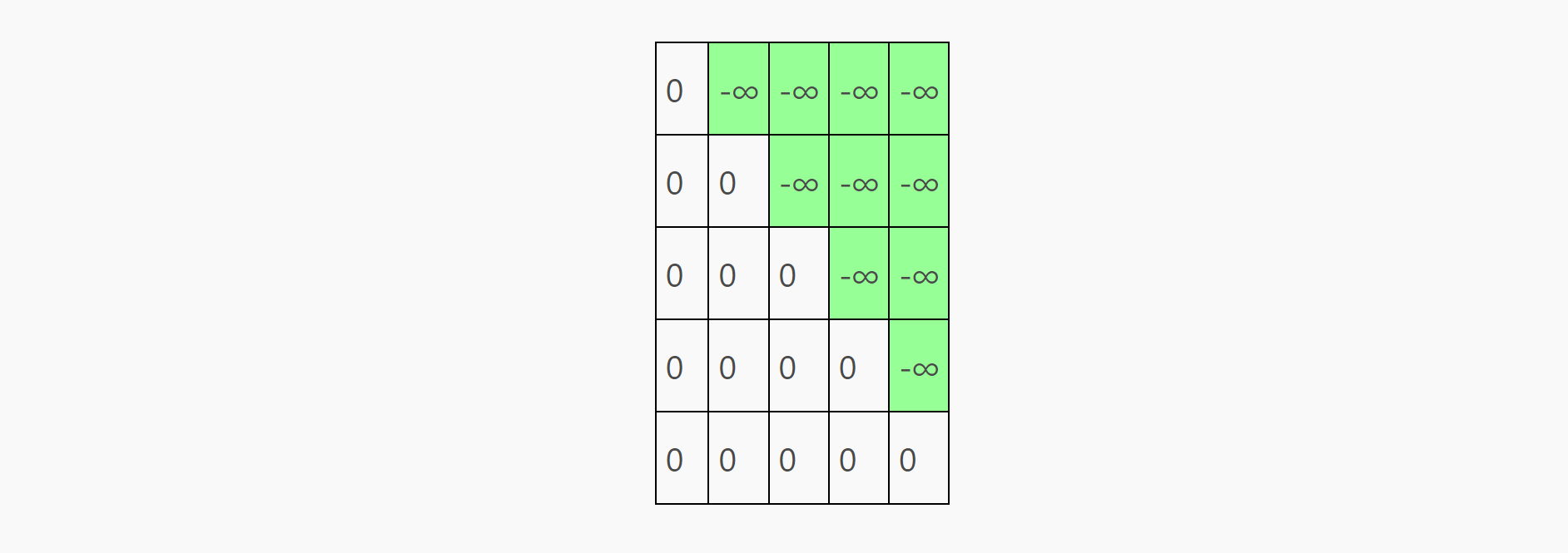
mask也防止模型在常规的梯度下降训练中作弊，如果没有mask模型会根据第二个token生成对第一个token的预测。在添加-∞后，这些位置的值会在softmax后被限制调整为0，这样保证里模型去真实地从前置序列中学习生成参数。

在我们的样例中，mask并不会做任何事情，因为手动生成的transformer模型不会说谎，但是我们仍然保留mask，以确保我们的模型结构与GPT-2相同。

softmax

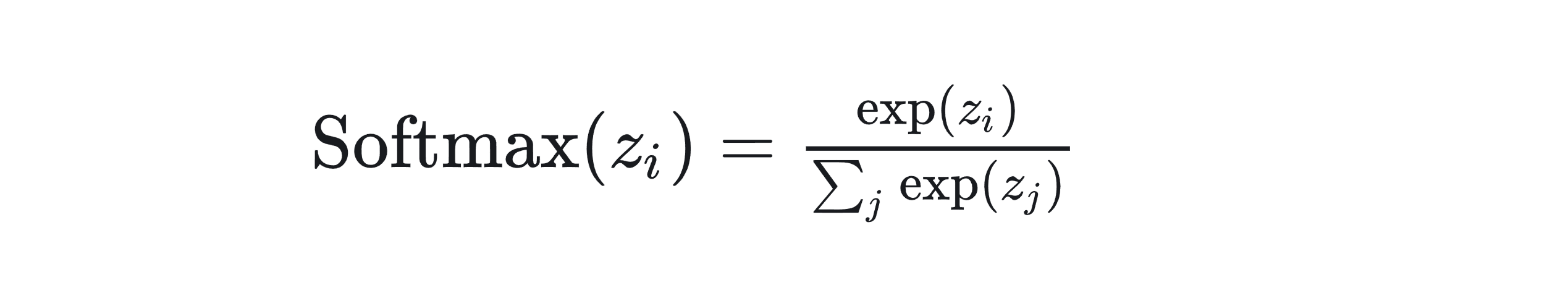
softmax是机器学习和深度学习中常用的一个函数，特别是在处理多分类问题时。softmax 函数可以将一个含任意实数的 K 维向量 “压缩” 到另一个 K 维实向量中，其中向量中的每个元素的取值都在 (0, 1) 之间，并且所有元素的和为 1。这使得 softmax 函数的输出可以被解释为一个概率分布。

softmax的代码定义为：

def softmax(x):
    exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True))
    return exp_x / np.sum(exp_x, axis=-1, keepdims=True)

代码解释如下：

1. def softmax(x):
   • 这一行定义了名为 softmax 的函数，它接收一个参数 x。x 可以是一个数、一个向量或者一个矩阵，表示输入到 softmax 函数的值。
2. exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True))
   • np.exp 计算 x 中每个元素的指数。x - np.max(x, axis=-1, keepdims=True) 这部分代码先从 x 中的每个元素中减去 x 在最后一个轴（axis=-1）上的最大值。这是为了数值稳定性，避免在计算指数时出现数值溢出。
   • axis=-1 指的是数组的最后一个维度，这样可以保证这个操作是在正确的维度上进行的，适用于处理多维数组。
   • keepdims=True 确保输出数组的维度与输入数组相同，这在后续的除法操作中保持了维度的一致性。
3. return exp_x / np.sum(exp_x, axis=-1, keepdims=True)
   • 这一行计算 softmax 函数的最终结果。np.sum(exp_x, axis=-1, keepdims=True) 计算 exp_x 在最后一个轴上的和，保持维度不变。然后，exp_x 中的每个元素都被这个和除以，从而得到 softmax 函数的输出。
   • 这样，输出的每个元素都是原始输入元素的指数与所有指数之和的比值，这保证了所有输出值的总和为 1，且每个值都在 (0, 1) 范围内。

这看起来很吓人，但是当你拆解后，softmax在做的事情为：

• 对于矩阵中的每一行；

• 从其他元素中减去该行中的最大值（除了最大的元素为 0，每个元素都将为负数）

• 计算每个元素的指数 (matrix[i, j] = e^matrix[i, j] )

  • 这使得最大的元素为 1，因为e^0 = 1
  • 略小于最大元素的值将接近 1，（例如 e^-0.5~=0.6)
  • 远小于最大元素的值将接近 0， (例如 e^-10~=0.00004)。

• 最后，我们将该行中的每个元素除以该行中所有值的总和，使该行的总和为 1（可以用作概率分布）

我们独立处理每一行，因为在我们的模型中，每一行都表示具有独立预测概率的token输入。

这是一个softmax的实例：

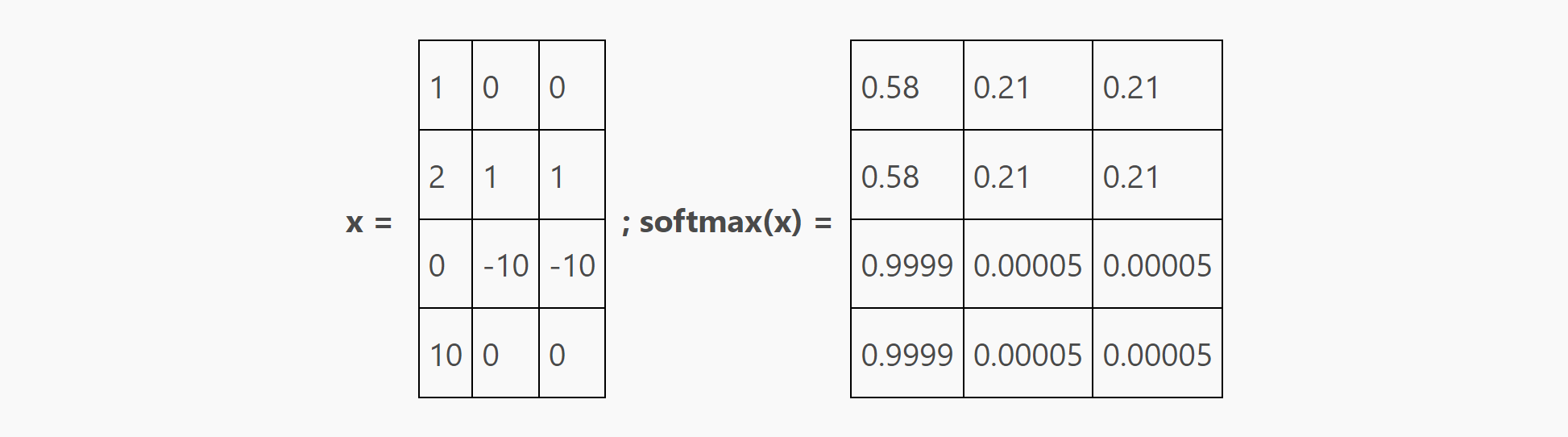
注意，每一行中最大的数值总会输出最大的softmax结果，但这个数值足够大时，这个softmax结果会接近100%。同时注意最大值的绝对大小并不重要，重要的是与其他值之间的相对大小关系，因为在第一步会减去最大值，即[10,0,0]会处理为[0.-10.-10]。

一个对softmax直观的理解是：softmax的工作类似于一个平滑的argmax，argmax将最大值映射到1，其他值映射到0-1的区间，但是softmax相对于argmax更加平滑。

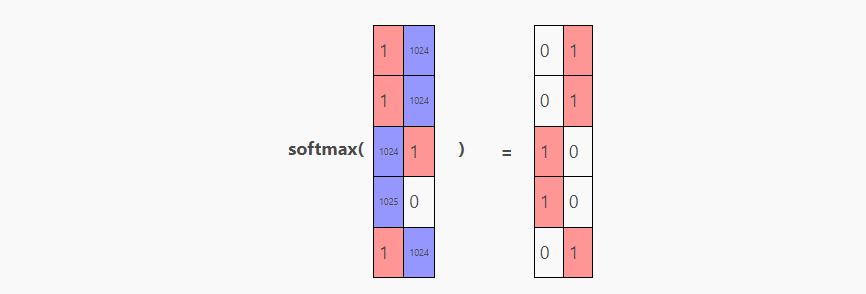
softmax(q @ k.T + mask)

softmax(q @ k.T + mask)的结果为:

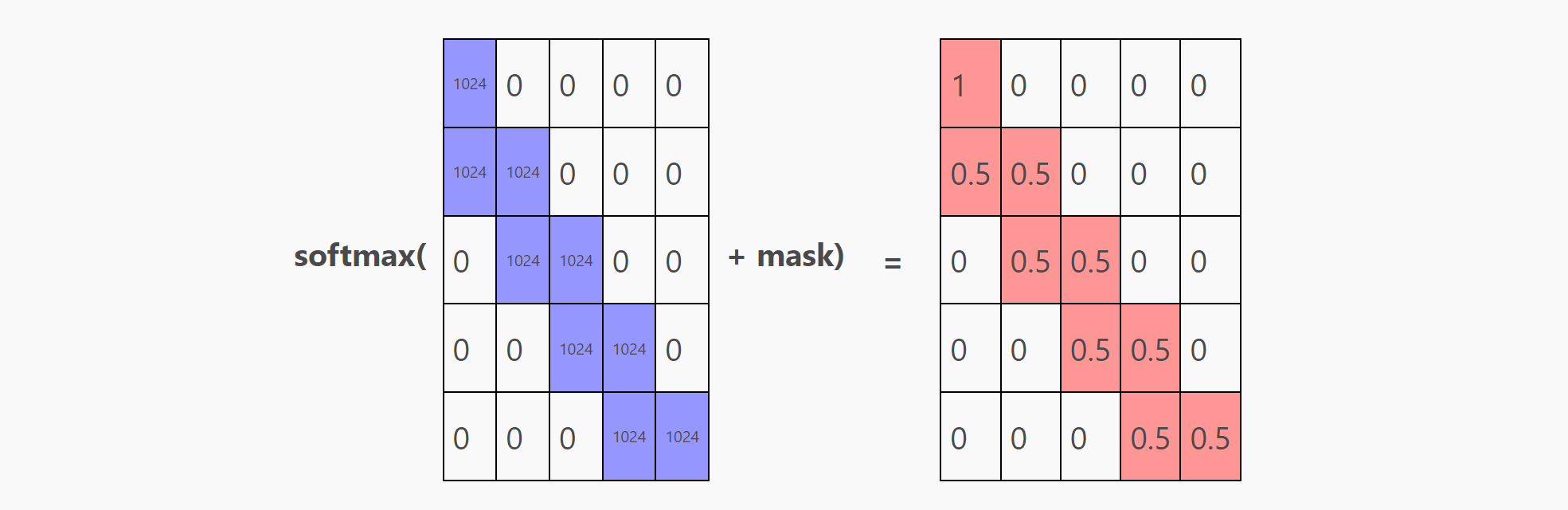
其中, 每一行都表示在模型在预测某一位置时，需要对不同位置token付出的注意力的多少。上图中，我们在做第一个预测时只需要关注第一个token，而当我们在做第二个及以后的预测时，需要同时关注当前位置的token与上一个位置的token。

关于mask和softmax的讨论到此为止，总的来说， softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) 的结果为：

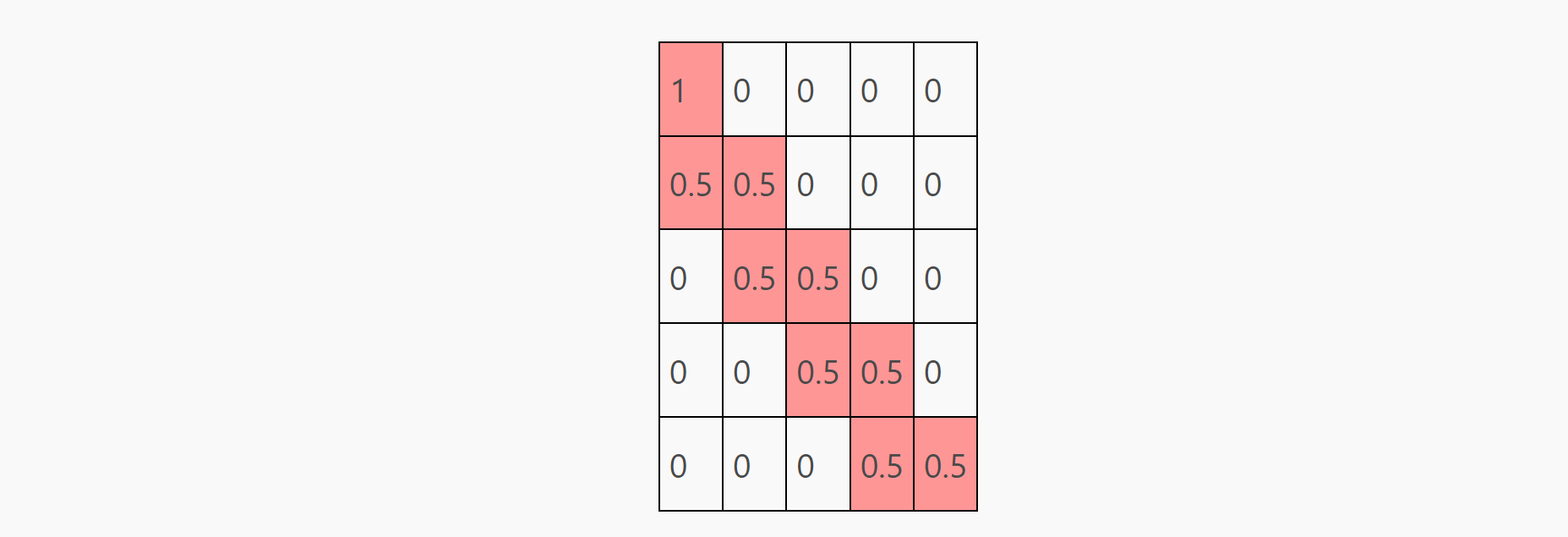
softmax(q @ k.T + mask) @ v

v是什么？attention的最后一步是将上面的矩阵与v进行乘积（ softmax(q @ k.T ) + mask) @ v），在这个公式中，v表示什么？

我们再回忆一下之前的embedding矩阵：

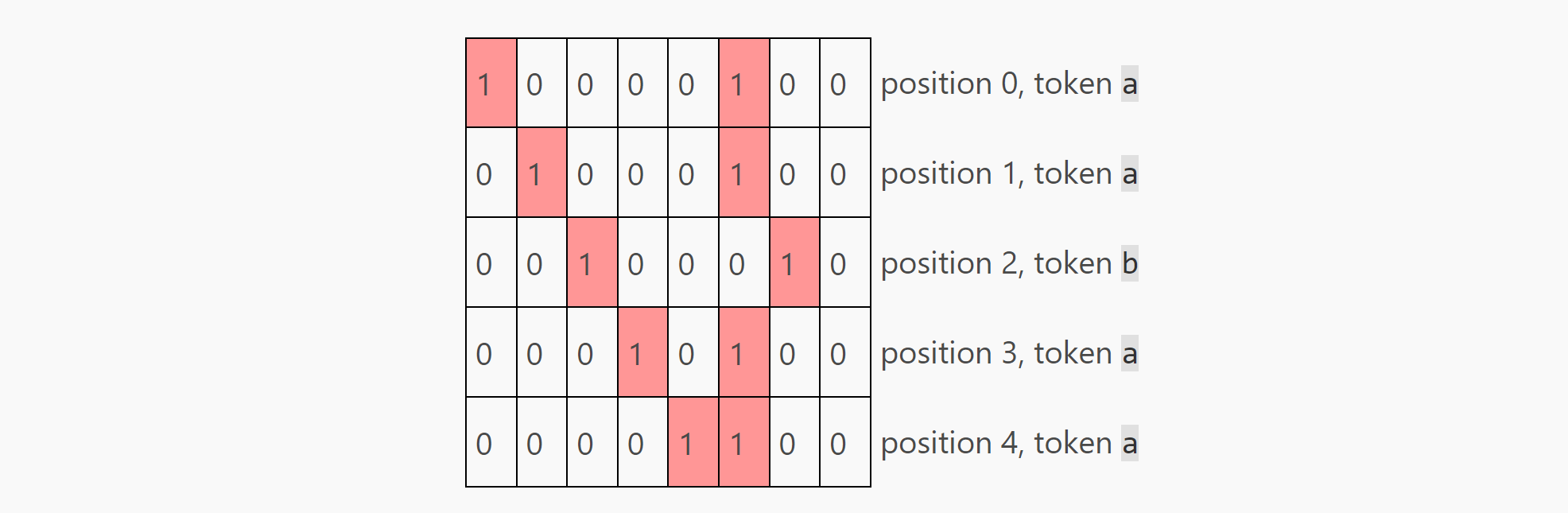
通过c_attn中的线性关系，我们得到下面这个qkv矩阵：

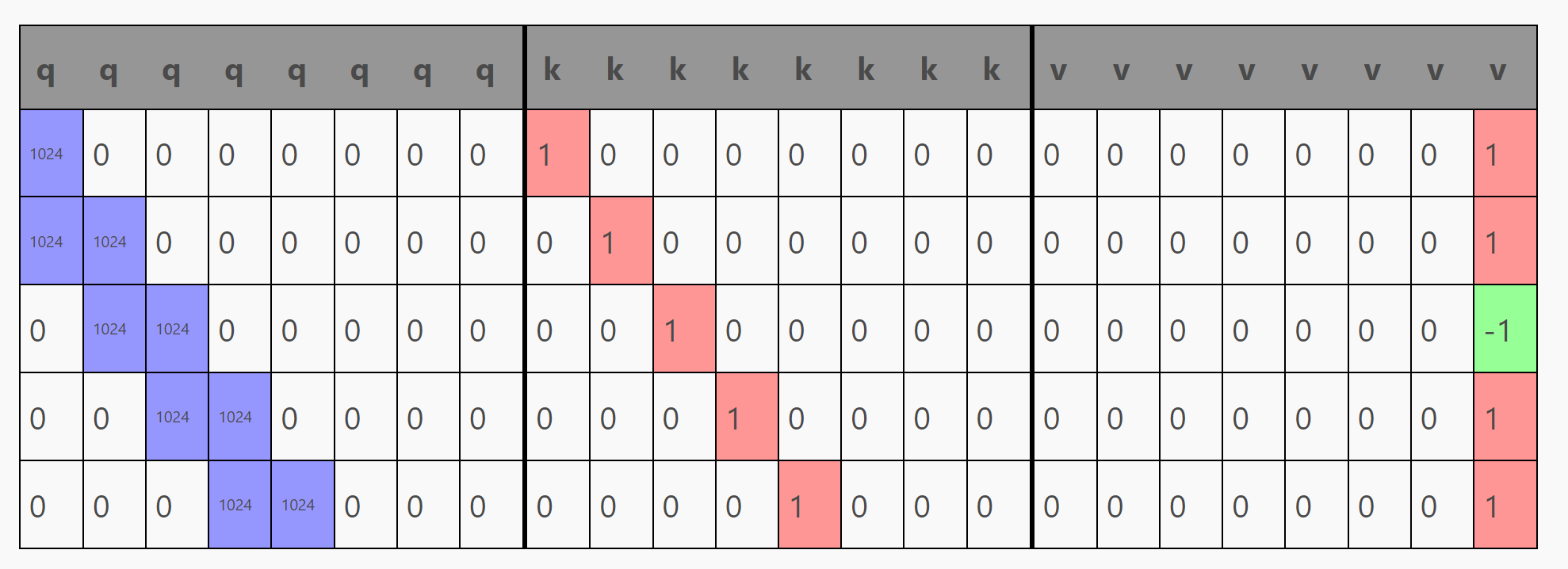
关注其中的v部分，我们看到这个矩阵只有第七列有元素，而且但token表示a时, 这个元素为1, 而当这个token表示b时, 这个元素为-1。这意味着，v是由之前的 one-hot encoding（a = [1, 0], b = [0, 1]）转化而来。

回想我们预测aabaab的任务，或者说下面这个任务：

• if previous tokens are (a, a) => predict b
• if previous tokens are (a, b) => predict a
• if previous tokens are (b, a) => predict a
• if previous tokens are (b, b) => error, out of domain

因为bb是非法的，所以我们只需要在当前两个token是相同的前提下预测b，而矩阵乘法包含求和，这就意味着我们可以用加法抵消，也就是: 0.5 + 0.5 = 1, 0.5 + (-0.5) = 0。

我们定义, 对于当前需要预测的元素, 其之前的两个元素分别为t[-2] t[-1]. 同时我们定义一个函数 output = t[-2]+ t[-1]

通过对（a = 1，b = -1）编码，这个简单的等式正好就能满足我们的需求。等式的值为0时, 预测值为a，等式值为1时, 预测值为b.

• a, b → 0.5 * 1 + 0.5 * (-1) = 0 → a
• b, a → 0.5 * (-1) + 0.5 * 1 = 0 → a
• a, a → 0.5 * 1 + 0.5 * 1 = 1 → b

使用我们之前softmax矩阵的结果并且将其与分割下来的v矩阵进行乘积，对每一行进行计算后，对于aabaa这个输入，我们会得到一下这个结果：

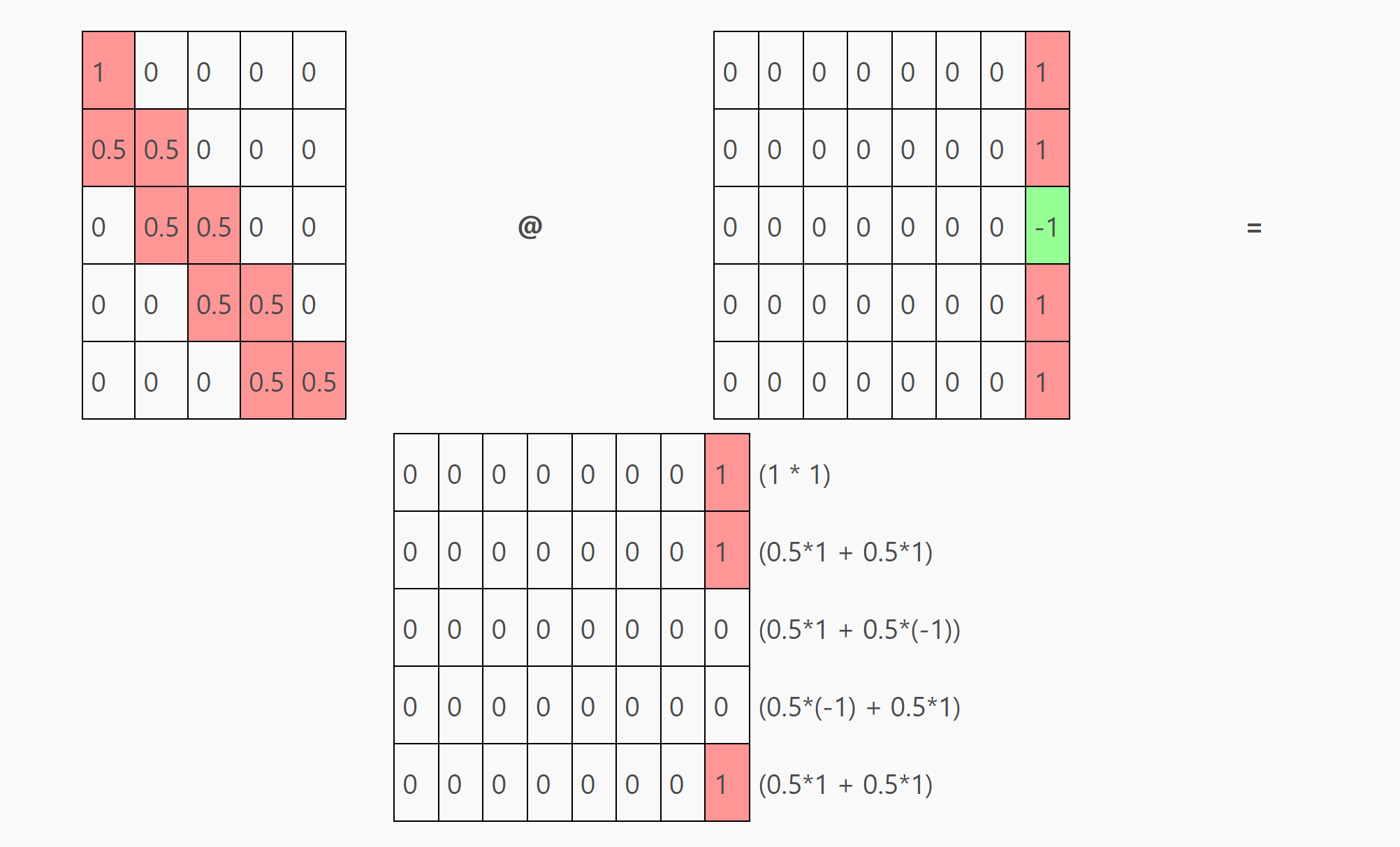
最后一列的结果为：11001，即预测结果为bbaab，正确结果应为abaab。预测的第一个b错误，这个因为此处没有足够的数据支撑（前面只有一个a，下一个元素可以是a也可以是b），其余的预测都是正确的。

Summary

总的来说，c_attn主要做的工作是：

• 将位置编码映射到”attention window”中的q
• 将位置编码提取到k
• 将v中的token embedding转化为1/-1
• 使用softmax将q和k合并（softmax(q @ k.T / ... + mask)），我们得到一个seq_len x seq_len大小的矩阵
  • 在第一行，只关注第一个token
  • 在其余行，平等关注当前token和上一个token
• 最终，通过softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) @ v，使用加法抵消得到
  • 每行中第七个元素是0时代表预测下一个元素为a
  • 每行中第七个元素是1时代表预测下一个元素为b

我们关于attention部分的讨论就此为止。

Projecting back to embedding space

为了完成transformer模块，我们需要将attention的结果返回到常规编码中。我们的attention头将预测结果存放于 embedding[row, 7] (1 for b, 0 for a)。但是在embedding中我们使用了one-hot策略，这个策略在embedding[row, 5]存放一个正值以表示a，在embedding[row, 6]存放一个正值以表示b。

由于某些原因（稍后解释），我们不想在让这层表示为： [..., 1, 0, ...] or [..., 0, 1, ...]，我们想让其表示为： [..., 1024, 0, ...] or [..., 0, 1024, ...]。

为了完成这点，我们需要做的是使用c_proj的偏置去将embedding[row, 5]的默认值设置为1024。并且适当缩放attention的结果并嵌入 embedding[row, 7]。

Lg = 1024  # Large

MODEL = {
  "wte": ...,
  "wpe": ...,
  "blocks": [
    {
      "attn": {
        "c_attn": ...,
        "c_proj": {  # weights to project attn result back to embedding space
          "b": [0, 0, 0, 0, 0, Lg, 0, 0],
          "w": np.array([
            [0, 0, 0, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 0, -Lg, Lg, 0],
          ]),
        },
      },
    },
  ],
}

换句话说，在经过 c_proj之后,

• embedding[row, 5] (表示 a) 等同于Lg + (-Lg) * prediction
• embedding[row, 6] (表示 b) 等同于0 + Lg * prediction

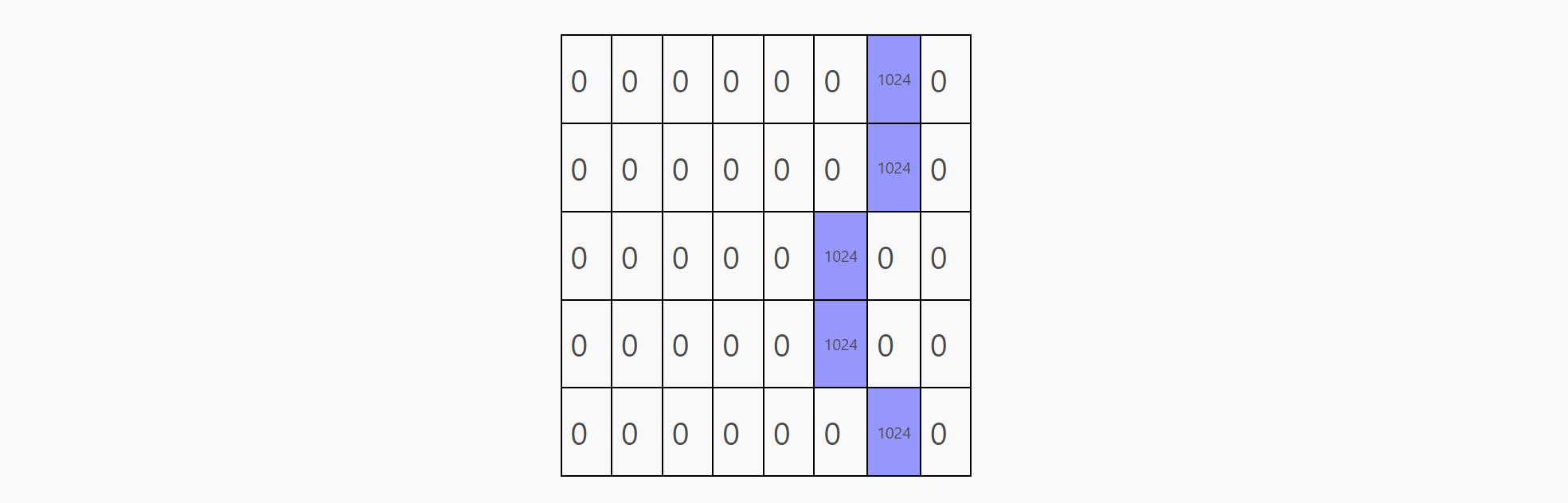
在将attention的结果通过c_proj处理后，我们得到了这个矩阵，这个正是我们所需要的，被缩放1024倍、one-hot模式预测的矩阵。

Residual connection

残差链接可以帮助深度神经网络维持主要的信息流通过大量的层/我们将原始输入添加到输出的过程成为残差连接, 也就是将c_proj的原始输入添加到了c_proj的输出中。

体现在 transformer_block中，我们使用 x = x + causal_self_attention(x, ...) 而不是简单的 x = causal_self_attention(x, ...)。

但是在我们的样例中，这并没有什么作用. 这就是为什么 c_proj 的输出被缩放了1024倍：为了排除不需要的残差链接的影响。

经过残差连接后, transformer模块的最终输出为:

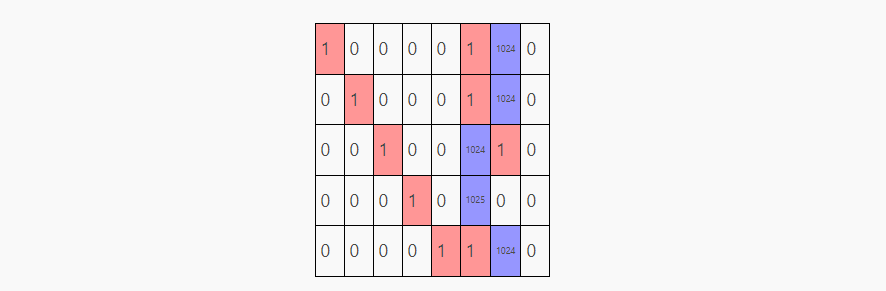
Projecting back to vocabulary space

将transformer模块的输出的结果矩阵与转置后的token embedding weights (wte)相乘，来得到最终的结果。

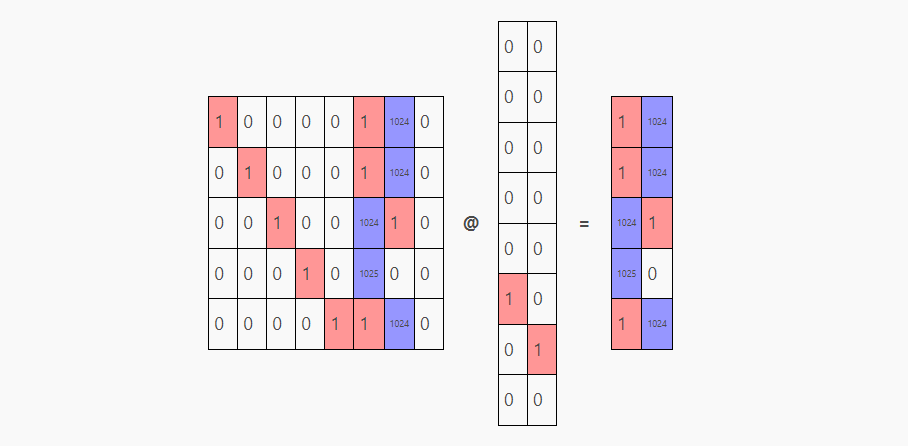
结果中的红色部分表示模型由于残差连接而略微倾向于重复一个token。但是相较于1024的输出，最终预测结果经过softmax后仍然100%倾向于某个词。

也就是说，当给到aabaa序列时，模型会预测为：

• a 后面的标记是 b（可以接受，二者皆可）
• aa 后面的标记是 b（正确！）。
• aab 后面的标记是 a（正确！）。
• aaba 后面的标记是 a（正确！）。
• aabaa 后面的标记是 b（正确！）。

当然了，对于模型推理来说，我们只关心最后一行的预测结果：aabaa后是a。其他预测只对模型训练有用。

在设置完成所有的模型权重之后，我们可以写一个complete函数来证明我们模型输出的正确性：

def complete(s, max_new_tokens=10):
  tokens = tokenize(s)
  while len(tokens) < len(s) + max_new_tokens:
    logits = gpt(np.array(tokens[-5:]), **MODEL)
    probs = softmax(logits)
    pred = np.argmax(probs[-1]) # greedy sample, but temperature sampling would give the same results in our case
    tokens.append(pred)
  return s + " :: " + "".join(untok(t) for t in tokens[len(s):])

print(complete("a")) # a :: baabaabaab
print(complete("ba")) # ba :: abaabaabaa
print(complete("abaab")) # abaab :: aabaabaaba

这个模型甚至能从错误的输出中恢复，以输出正确的答案。

如果我们写一个小型的测试循环对模型进行测试，这个手工制作的模型具有100%的正确率（只要有明确的上下文）。

test = "aab" * 10
total, correct = 0, 0
for i in range(2, len(test) - 1):
  ctx = test[:i]
  expected = test[i]
  total += 1
  if untok(predict(ctx)) == expected:
    correct += 1
print(f"ACCURACY: {correct / total * 100}% ({correct} / {total})")
# ACCURACY: 100.0% (27 / 27)

Completed code

# Model ops from https://github.com/jaymody/picoGPT/blob/main/gpt2.py (MIT license)

import numpy as np


def softmax(x):
    exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True))
    return exp_x / np.sum(exp_x, axis=-1, keepdims=True)

# [m, in], [in, out], [out] -> [m, out]
def linear(x, w, b):
    return x @ w + b

# [n_q, d_k], [n_k, d_k], [n_k, d_v], [n_q, n_k] -> [n_q, d_v]
def attention(q, k, v, mask):
    return softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) @ v

# [n_seq, n_embd] -> [n_seq, n_embd]
def causal_self_attention(x, c_attn, c_proj):
    # qkv projections
    x = linear(x, **c_attn)  # [n_seq, n_embd] -> [n_seq, 3*n_embd]

    # split into qkv
    q, k, v = np.split(x, 3, axis=-1)  # [n_seq, 3*n_embd] -> 3 of [n_seq, n_embd]

    # causal mask to hide future inputs from being attended to
    causal_mask = (1 - np.tri(x.shape[0], dtype=x.dtype)) * -1e10  # [n_seq, n_seq]

    # perform causal self attention
    x = attention(q, k, v, causal_mask)  # [n_seq, n_embd] -> [n_seq, n_embd]

    # out projection
    x = linear(x, **c_proj)  # [n_seq, n_embd] @ [n_embd, n_embd] = [n_seq, n_embd]

    return x

# [n_seq, n_embd] -> [n_seq, n_embd]
def transformer_block(x, attn):
    x = x + causal_self_attention(x, **attn)
    # NOTE: removed ffn
    return x

# [n_seq] -> [n_seq, n_vocab]
def gpt(inputs, wte, wpe, blocks):
    # token + positional embeddings
    x = wte[inputs] + wpe[range(len(inputs))]  # [n_seq] -> [n_seq, n_embd]

    # forward pass through n_layer transformer blocks
    for block in blocks:
        x = transformer_block(x, **block)  # [n_seq, n_embd] -> [n_seq, n_embd]

    # projection to vocab
    return x @ wte.T  # [n_seq, n_embd] -> [n_seq, n_vocab]


N_CTX = 5
N_VOCAB = 2
N_EMBED = 8

Lg = 1024  # Large

MODEL = {
    # EMBEDDING USAGE
    #  P = Position embeddings (one-hot)
    #  T = Token embeddings (one-hot, first is `a`, second is `b`)
    #  V = Prediction scratch space
    #
    #       [P, P, P, P, P, T, T, V]
    "wte": np.array(
        # one-hot token embeddings
        [
            [0, 0, 0, 0, 0, 1, 0, 0],  # token `a` (id 0)
            [0, 0, 0, 0, 0, 0, 1, 0],  # token `b` (id 1)
        ]
    ),
    "wpe": np.array(
        # one-hot position embeddings
        [
            [1, 0, 0, 0, 0, 0, 0, 0],  # position 0
            [0, 1, 0, 0, 0, 0, 0, 0],  # position 1
            [0, 0, 1, 0, 0, 0, 0, 0],  # position 2
            [0, 0, 0, 1, 0, 0, 0, 0],  # position 3
            [0, 0, 0, 0, 1, 0, 0, 0],  # position 4
        ]
    ),
    "blocks": [
        {
            "attn": {
                "c_attn": {  # generates qkv matrix
                    "b": np.zeros(N_EMBED * 3),
                    "w": np.array(
                        # this is where the magic happens
                        # fmt: off
                        [
                          [Lg, 0., 0., 0., 0., 0., 0., 0.,  # q
                            1., 0., 0., 0., 0., 0., 0., 0.,  # k
                              0., 0., 0., 0., 0., 0., 0., 0.], # v
                          [Lg, Lg, 0., 0., 0., 0., 0., 0.,  # q
                            0., 1., 0., 0., 0., 0., 0., 0.,  # k
                              0., 0., 0., 0., 0., 0., 0., 0.], # v
                          [0., Lg, Lg, 0., 0., 0., 0., 0.,  # q
                            0., 0., 1., 0., 0., 0., 0., 0.,  # k
                              0., 0., 0., 0., 0., 0., 0., 0.], # v
                          [0., 0., Lg, Lg, 0., 0., 0., 0.,  # q
                            0., 0., 0., 1., 0., 0., 0., 0.,  # k
                              0., 0., 0., 0., 0., 0., 0., 0.], # v
                          [0., 0., 0., Lg, Lg, 0., 0., 0.,  # q
                            0., 0., 0., 0., 1., 0., 0., 0.,  # k
                              0., 0., 0., 0., 0., 0., 0., 0.], # v
                          [0., 0., 0., 0., 0., 0., 0., 0.,  # q
                            0., 0., 0., 0., 0., 0., 0., 0.,  # k
                              0., 0., 0., 0., 0., 0., 0., 1.], # v
                          [0., 0., 0., 0., 0., 0., 0., 0.,  # q
                            0., 0., 0., 0., 0., 0., 0., 0.,  # k
                              0., 0., 0., 0., 0., 0., 0., -1], # v
                          [0., 0., 0., 0., 0., 0., 0., 0.,  # q
                            0., 0., 0., 0., 0., 0., 0., 0.,  # k
                              0., 0., 0., 0., 0., 0., 0., 0.], # v
                        ]
                        # fmt: on
                    ),
                },
                "c_proj": {  # weights to project attn result back to embedding space
                    "b": [0, 0, 0, 0, 0, Lg, 0, 0],
                    "w": np.array(
                        [
                            [0, 0, 0, 0, 0, 0, 0, 0],
                            [0, 0, 0, 0, 0, 0, 0, 0],
                            [0, 0, 0, 0, 0, 0, 0, 0],
                            [0, 0, 0, 0, 0, 0, 0, 0],
                            [0, 0, 0, 0, 0, 0, 0, 0],
                            [0, 0, 0, 0, 0, 0, 0, 0],
                            [0, 0, 0, 0, 0, 0, 0, 0],
                            [0, 0, 0, 0, 0, -Lg, Lg, 0],
                        ]
                    ),
                },
            },
        }
    ],
}

CHARS = ["a", "b"]
def tokenize(s): return [CHARS.index(c) for c in s]
def untok(tok): return CHARS[tok]

def predict(s):
    tokens = tokenize(s)[-5:]
    logits = gpt(np.array(tokens), **MODEL)
    probs = softmax(logits)

    for i, tok in enumerate(tokens):
        pred = np.argmax(probs[i])
        print(
            f"{untok(tok)} ({tok}): next={untok(pred)} ({pred}) probs={probs[i]} logits={logits[i]}"
        )

    return np.argmax(probs[-1])

def complete(s, max_new_tokens=10):
    tokens = tokenize(s)
    while len(tokens) < len(s) + max_new_tokens:
        logits = gpt(np.array(tokens[-5:]), **MODEL)
        probs = softmax(logits)
        pred = np.argmax(probs[-1])
        tokens.append(pred)
    return s + " :: " + "".join(untok(t) for t in tokens[len(s):])

test = "aab" * 10
total, correct = 0, 0
for i in range(2, len(test) - 1):
    ctx = test[:i]
    expected = test[i]
    total += 1
    if untok(predict(ctx)) == expected:
        correct += 1
print(f"ACCURACY: {correct / total * 100}% ({correct} / {total})")

Others

为了保证整体结构清晰,我删去了一些GPT-2中的结构，包括：

• 去掉了层归一化，因为它们很难处理。我想要传递漂亮的矩阵，里面有很多0和1，容易推理，但是层归一化却想要把我的 1 和 0 变成 1.73200462 和 -0.57733487：

pythonCopy codedef layer_norm(x, g, b, eps: float = 1e-5):
  mean = np.mean(x, axis=-1, keepdims=True)
  variance = np.var(x, axis=-1, keepdims=True)
  # 对x进行归一化，使得最后一个轴上的均值为0，方差为1
  x = (x - mean) / np.sqrt(variance + eps)
  return g * x + b  # 使用gamma/beta参数进行缩放和偏移

（我本可以通过将 gamma 分配回 np.sqrt(...) 缩放来逆转效果，将 beta 分配回 (x - mean) 偏移来逆转效果，但是与其每次进行无关的更改时都修复它们，不如直接完全移除层归一化更容易。）

• 使用了单头注意力而不是多头注意力，因为不需要多个头。
• 去掉了变压器块中的 mlp 前馈层，因为我不需要它。（尽管我可以将它设置为单位矩阵。）

不像一些其他变压器架构，GPT-2 使用纯学习的位置嵌入，所以这里没有任何正弦或 RoPEs。

实际上，q 或 k 不需要担任这些角色——在这篇文章的原始版本中，我把它们颠倒了，q 是提取的位置嵌入，k 是查询。但是，现在文章中的方式更常见，更适合矩阵名称——尽管 GPT-2 从来没听说过那些名称 ;-)

实际上，代码中使用的不是 -∞，而是像 -1e10 这样的数字，以避免 NaN 的问题，但实际效果是一样的。